Sudoku
It is well known that the number-placement puzzle Sudoku can be formulated as a binary optimization problem. The following optimization problem formulation is from Bartlett et al. (2008).
\[ \begin{array}{rl} \underset{x}{\text{minimize}} & \mathbb{0}^\top x \\ \text{subject to} & x_{ijk} \in \{0, 1\} \\ \text{only one k in each column:} & \sum_{i=1}^9 x_{ijk} = 1, ~~~~ j = 1:9,~ k = 1:9 \\ \text{only one k in each row:} & \sum_{j=1}^9 x_{ijk} = 1, ~~~~ i = 1:9,~ k = 1:9 \\ \text{only one k in each block:} & \sum_{j = 3 (q - 1) + 1}^{3 q} \sum_{i = 3(p - 1) + 1}^{3 p} x_{ijk} = 1, ~~~~ k = 1:9,~ p = 1:3,~ q = 1:3 \\ \text{exactly one number for each position:} & \sum_{k=1}^9 x_{ijk} = 1, ~~~~ i = 1:9,~ j = 1:9 \\ \text{stating values are fixed:} & x_{ijk} = 1 ~~~ \forall (i, j, k) \\ \end{array} \]
In R the packages sudoku and sudokuAlt can be used to generate and solve Sudoku puzzles.
library(sudokuAlt)
sudoku_puzzle <- makeGame()
plot(sudoku_puzzle)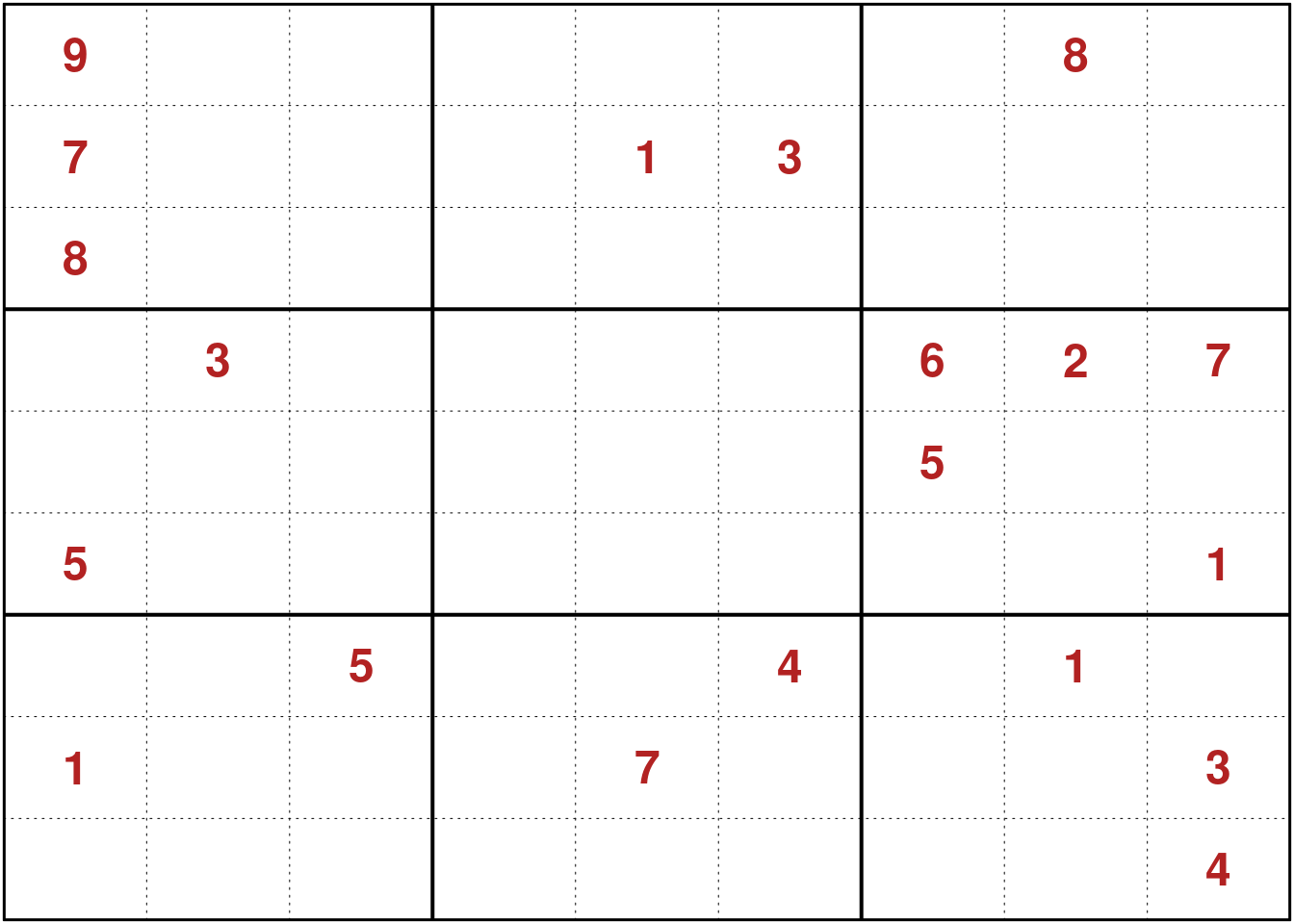
library(slam)
library(ROI)
library(ROI.plugin.msbinlp)
library(ROI.plugin.glpk)Auxiliary functions
as.matrix.sudoku <- function(x) matrix(as.numeric(x), 9, 9)
to_col_index <- function(i, j, v) {
(v - 1) * 81 + (i - 1) * 9 + j
}
index_to_triplet <- function(idx) {
.index_to_triplet <- function(idx) {
v <- (idx - 1) %/% 81 + 1
idx <- idx - (v - 1) * 81
i <- (idx - 1)%/% 9 + 1
idx <- idx - (i - 1) * 9
c(i = i, j = idx, v = v)
}
t(sapply(idx, .index_to_triplet))
}
solve_sudoku <- function(M, solver, solve = TRUE, ...) {
stm <- simple_triplet_matrix
seq9_9 <- rep(1:9, 9)
seq9_9e <- rep(1:9, each = 9)
seq81_9e <- rep(seq_len(81), each = 9)
ones729 <- rep.int(1, 9^3)
M <- as.matrix(M)
M[is.na(M)] <- 0
M <- as.simple_triplet_matrix(M)
## setup OP
op <- OP(double(9^3))
## basic setting (fixed coefficients)
j <- mapply(to_col_index, M$i, M$j, M$v)
nfv <- length(M$i) ## number of fixed variables
A0 <- stm(i = seq_len(nfv), j = j, v = rep.int(1, nfv), ncol = 9^3)
LC0 <- L_constraint(A0, eq(nfv), rep.int(1, nfv))
## sum_{i=1:n} x_ijk = 1, j = 1:n, k = 1:n
only_one_k_in_each_column <- function(j, k) {
sapply(1:9, function(i) to_col_index(i, j, k))
}
j <- unlist(mapply(only_one_k_in_each_column, seq9_9e, seq9_9, SIMPLIFY = FALSE))
A1 <- stm(i = seq81_9e, j = j, v = ones729, nrow = 81, ncol = 9^3)
## sum_{j=1:n} x_ijk = 1
only_one_k_in_each_row <- function(i, k) {
sapply(1:9, function(j) to_col_index(i, j, k))
}
j <- unlist(mapply(only_one_k_in_each_row, seq9_9e, seq9_9, SIMPLIFY = FALSE))
A2 <- stm(i = seq81_9e, j = j, v = ones729, nrow = 81, ncol = 9^3)
only_one_k_in_each_submatrix <- function(blocki, blockj, k) {
i <- (blocki - 1) * 3 + 1:3
j <- (blockj - 1) * 3 + 1:3
coo <- expand.grid(i = i, j = j, v = k)
mapply(to_col_index, i = coo$i, j = coo$j, v = coo$v)
}
coo <- expand.grid(i = 1:3, j = 1:3, k = 1:9)
j <- unlist(mapply(only_one_k_in_each_submatrix,
blocki = coo$i, blockj = coo$j, k = coo$k, SIMPLIFY = FALSE))
A3 <- stm(i = seq81_9e, j = j, v = ones729, ncol = 9^3)
## at every position in the matrix must be one value
fill_matrix <- function(i, j) {
sapply(1:9, function(k) to_col_index(i, j, k))
}
j <- unlist(mapply(fill_matrix, i = seq9_9e, j = seq9_9, SIMPLIFY = FALSE))
A4 <- stm(i = seq81_9e, j = j, v = ones729, ncol = 9^3)
A <- rbind(A1, A2, A3, A4)
LC1 <- L_constraint(A, eq(nrow(A)), rep.int(1, nrow(A)))
constraints(op) <- rbind(LC0, LC1)
types(op) <- rep.int("B", 9^3)
if (!solve) return(op)
s <- ROI_solve(op, solver = solver, ...)
sol <- solution(s)
to_sudoku_solution <- function(sol) {
coo <- index_to_triplet(which(as.logical(sol)))
sudoku_solution <- as.matrix(stm(coo[,1], coo[,2], coo[,3]), nrow = 9, ncol = 9)
structure(sudoku_solution, class = c("sudoku", "matrix"))
}
if ( any(lengths(sol) > 1L) & length(sol) > 1L ) {
lapply(solution(s), to_sudoku_solution)
} else {
if ( length(sol) == 1L ) {
to_sudoku_solution(sol[[1L]])
} else {
to_sudoku_solution(sol)
}
}
}
sudoku_is_valid_solution <- function(x) {
.sudoku_is_valid_solution <- function(x) {
stopifnot(inherits(x, "sudoku"))
seq19 <- seq_len(9)
for (i in seq19) {
if ( any(sort(as.vector(x[i, ])) != seq19) ) return(FALSE)
if ( any(sort(as.vector(x[, i])) != seq19) ) return(FALSE)
}
for (i in 1:3) {
for (j in 1:3) {
block <- x[(i-1) * 3 + 1:3, (j-1) * 3 + 1:3]
if ( any(sort(as.vector(block)) != seq19) ) return(FALSE)
}
}
return(TRUE)
}
if ( is.list(x) ) {
sapply(x, .sudoku_is_valid_solution)
} else {
.sudoku_is_valid_solution(x)
}
}Solve Sudoku
We now solve the previously defined Sudoku.
sudoku_solution <- solve_sudoku(sudoku_puzzle, solver = "glpk")
sudoku_is_valid_solution(sudoku_solution)## [1] TRUEplot(sudoku_solution)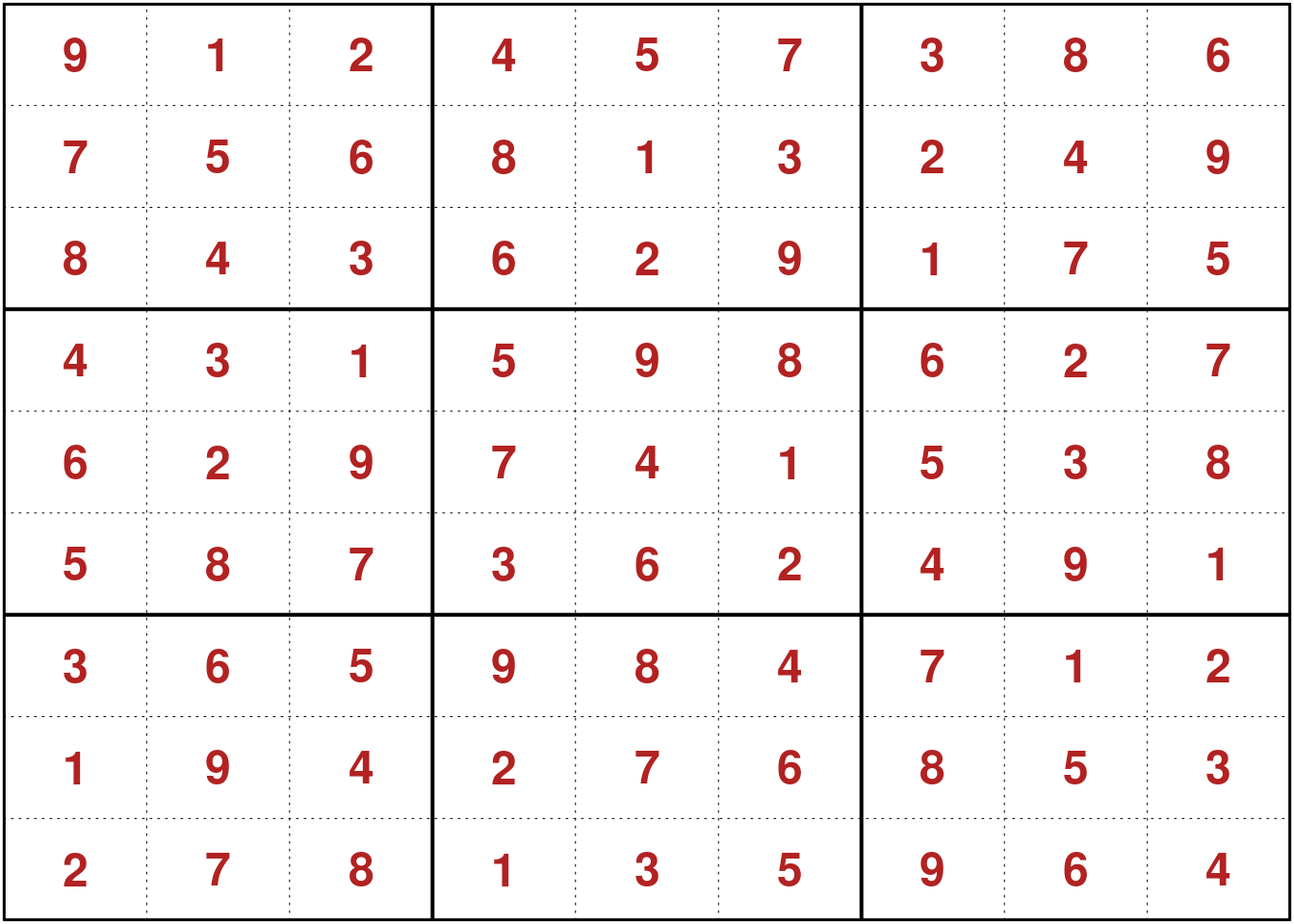
Furthermore it is easy to check if there exist multiple solutions to the Sudoku. Here we only want to obtain up to 10 solution to obtain all set the maximum number of solutions to infinity (nsol_max = Inf).
sudoku_solution <- solve_sudoku(sudoku_puzzle, solver = "msbinlp", nsol_max = 10L)
sudoku_solution## [[1]]
##
## + - - - + - - - + - - - +
## | 9 1 2 | 4 5 7 | 3 8 6 |
## | 7 5 6 | 8 1 3 | 2 4 9 |
## | 8 4 3 | 6 2 9 | 1 7 5 |
## + - - - + - - - + - - - +
## | 4 3 1 | 5 9 8 | 6 2 7 |
## | 6 2 9 | 7 4 1 | 5 3 8 |
## | 5 8 7 | 3 6 2 | 4 9 1 |
## + - - - + - - - + - - - +
## | 3 6 5 | 9 8 4 | 7 1 2 |
## | 1 9 4 | 2 7 6 | 8 5 3 |
## | 2 7 8 | 1 3 5 | 9 6 4 |
## + - - - + - - - + - - - +
##
## [[2]]
##
## + - - - + - - - + - - - +
## | 9 1 2 | 4 6 7 | 3 8 5 |
## | 7 5 6 | 8 1 3 | 2 4 9 |
## | 8 4 3 | 2 5 9 | 1 7 6 |
## + - - - + - - - + - - - +
## | 4 3 8 | 1 9 5 | 6 2 7 |
## | 2 7 1 | 3 4 6 | 5 9 8 |
## | 5 6 9 | 7 2 8 | 4 3 1 |
## + - - - + - - - + - - - +
## | 6 8 5 | 9 3 4 | 7 1 2 |
## | 1 9 4 | 5 7 2 | 8 6 3 |
## | 3 2 7 | 6 8 1 | 9 5 4 |
## + - - - + - - - + - - - +
##
## [[3]]
##
## + - - - + - - - + - - - +
## | 9 1 3 | 4 2 6 | 7 8 5 |
## | 7 5 2 | 8 1 3 | 4 6 9 |
## | 8 6 4 | 7 5 9 | 1 3 2 |
## + - - - + - - - + - - - +
## | 4 3 8 | 5 9 1 | 6 2 7 |
## | 6 2 1 | 3 4 7 | 5 9 8 |
## | 5 9 7 | 2 6 8 | 3 4 1 |
## + - - - + - - - + - - - +
## | 3 7 5 | 9 8 4 | 2 1 6 |
## | 1 4 9 | 6 7 2 | 8 5 3 |
## | 2 8 6 | 1 3 5 | 9 7 4 |
## + - - - + - - - + - - - +
##
## [[4]]
##
## + - - - + - - - + - - - +
## | 9 2 3 | 4 5 7 | 1 8 6 |
## | 7 5 6 | 8 1 3 | 4 9 2 |
## | 8 1 4 | 2 9 6 | 3 7 5 |
## + - - - + - - - + - - - +
## | 4 3 1 | 9 8 5 | 6 2 7 |
## | 2 9 7 | 6 3 1 | 5 4 8 |
## | 5 6 8 | 7 4 2 | 9 3 1 |
## + - - - + - - - + - - - +
## | 6 8 5 | 3 2 4 | 7 1 9 |
## | 1 4 2 | 5 7 9 | 8 6 3 |
## | 3 7 9 | 1 6 8 | 2 5 4 |
## + - - - + - - - + - - - +
##
## [[5]]
##
## + - - - + - - - + - - - +
## | 9 2 3 | 7 4 5 | 1 8 6 |
## | 7 5 6 | 8 1 3 | 2 4 9 |
## | 8 1 4 | 2 9 6 | 3 7 5 |
## + - - - + - - - + - - - +
## | 4 3 8 | 1 5 9 | 6 2 7 |
## | 2 6 1 | 4 3 7 | 5 9 8 |
## | 5 9 7 | 6 2 8 | 4 3 1 |
## + - - - + - - - + - - - +
## | 3 8 5 | 9 6 4 | 7 1 2 |
## | 1 4 9 | 5 7 2 | 8 6 3 |
## | 6 7 2 | 3 8 1 | 9 5 4 |
## + - - - + - - - + - - - +
##
## [[6]]
##
## + - - - + - - - + - - - +
## | 9 2 3 | 4 5 7 | 1 8 6 |
## | 7 5 6 | 8 1 3 | 2 4 9 |
## | 8 1 4 | 2 6 9 | 3 7 5 |
## + - - - + - - - + - - - +
## | 4 3 8 | 5 9 1 | 6 2 7 |
## | 2 7 1 | 3 4 6 | 5 9 8 |
## | 5 6 9 | 7 2 8 | 4 3 1 |
## + - - - + - - - + - - - +
## | 3 9 5 | 6 8 4 | 7 1 2 |
## | 1 4 2 | 9 7 5 | 8 6 3 |
## | 6 8 7 | 1 3 2 | 9 5 4 |
## + - - - + - - - + - - - +
##
## [[7]]
##
## + - - - + - - - + - - - +
## | 9 2 3 | 4 6 7 | 1 8 5 |
## | 7 5 6 | 8 1 3 | 9 4 2 |
## | 8 4 1 | 2 9 5 | 3 7 6 |
## + - - - + - - - + - - - +
## | 4 3 8 | 1 5 9 | 6 2 7 |
## | 2 1 7 | 3 4 6 | 5 9 8 |
## | 5 6 9 | 7 8 2 | 4 3 1 |
## + - - - + - - - + - - - +
## | 3 7 5 | 6 2 4 | 8 1 9 |
## | 1 9 4 | 5 7 8 | 2 6 3 |
## | 6 8 2 | 9 3 1 | 7 5 4 |
## + - - - + - - - + - - - +
##
## [[8]]
##
## + - - - + - - - + - - - +
## | 9 4 3 | 7 5 2 | 1 8 6 |
## | 7 2 6 | 8 1 3 | 9 4 5 |
## | 8 5 1 | 4 6 9 | 3 7 2 |
## + - - - + - - - + - - - +
## | 4 3 8 | 5 9 1 | 6 2 7 |
## | 2 1 7 | 3 4 6 | 5 9 8 |
## | 5 6 9 | 2 8 7 | 4 3 1 |
## + - - - + - - - + - - - +
## | 3 7 5 | 6 2 4 | 8 1 9 |
## | 1 8 4 | 9 7 5 | 2 6 3 |
## | 6 9 2 | 1 3 8 | 7 5 4 |
## + - - - + - - - + - - - +
##
## [[9]]
##
## + - - - + - - - + - - - +
## | 9 4 1 | 6 5 7 | 3 8 2 |
## | 7 6 2 | 8 1 3 | 4 9 5 |
## | 8 5 3 | 4 9 2 | 1 7 6 |
## + - - - + - - - + - - - +
## | 4 3 9 | 1 8 5 | 6 2 7 |
## | 2 1 8 | 7 4 6 | 5 3 9 |
## | 5 7 6 | 3 2 9 | 8 4 1 |
## + - - - + - - - + - - - +
## | 3 2 5 | 9 6 4 | 7 1 8 |
## | 1 9 4 | 5 7 8 | 2 6 3 |
## | 6 8 7 | 2 3 1 | 9 5 4 |
## + - - - + - - - + - - - +
##
## [[10]]
##
## + - - - + - - - + - - - +
## | 9 4 1 | 7 5 6 | 3 8 2 |
## | 7 2 6 | 8 1 3 | 9 4 5 |
## | 8 5 3 | 4 9 2 | 1 7 6 |
## + - - - + - - - + - - - +
## | 4 3 9 | 5 8 1 | 6 2 7 |
## | 6 1 2 | 3 4 7 | 5 9 8 |
## | 5 8 7 | 6 2 9 | 4 3 1 |
## + - - - + - - - + - - - +
## | 3 7 5 | 2 6 4 | 8 1 9 |
## | 1 6 4 | 9 7 8 | 2 5 3 |
## | 2 9 8 | 1 3 5 | 7 6 4 |
## + - - - + - - - + - - - +Solve a Sudoku from http://www.sudoku.org.uk/DailySudoku.asp
sudoku_puzzle <- fetchUKGame()Look if this Sudoku has a unique solution.
sudoku_solution <- solve_sudoku(sudoku_puzzle, solver = "msbinlp", nsol_max = 2L)
has_unique_solution <- inherits(sudoku_solution, "sudoku")
has_unique_solution## [1] TRUEReferences
- Bartlett, A., Chartier, T. P., Langville, A. N., & Rankin, T. D. (2008). An integer programming model for the Sudoku problem. Journal of Online Mathematics and its Applications, 8(1).
URLhttps://www.semanticscholar.org/paper/An-Integer-Programming-Model-for-the-Sudoku-Problem-Bartlett-Chartier/127ccaf7ebde0c47b36ae78cd1e2233b6061a57f